Big O Notation

Today we are going to talk about a very important topic when it comes to programming and making our code efficient. In programming, to detect the efficiency of an algorithm, we use what is called big O notation.

In the workplace or daily life, it might not seem as important, but certainly, in the vast majority of interviews, especially in "FAANG" interviews, having a clear understanding of this concept is crucial.

1 - What is big O notation?

Big O notation is a system that allows us to compare two algorithms. By understanding the notation, we are able to analyze the best scenario, so when we have multiple options, we can choose the most effective one and the one that will work best under heavy load.

When we define the efficiency of an algorithm, we do not do it by indicating the exact number of steps, such as "an algorithm with 200 steps and another with 120 steps." This is because the number of steps cannot be reduced to a single value for all cases.

For example, if we use a linear search algorithm (that is, it checks each element of a list one by one), this algorithm takes 200 steps for an array with 200 elements, and 120 steps for an array with 120 elements in the worst scenario.

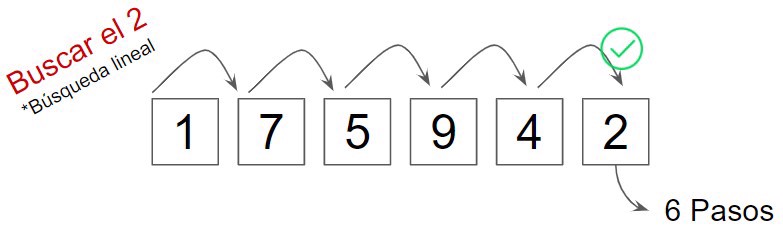
To simplify and improve communication about algorithm complexity, we use a mathematical concept called "Big O notation." For this post, you don't need to know mathematics, as I will reduce the mathematical concepts to the essentials.

Once we understand how big O notation works, analyzing algorithms becomes much easier, which can always help when writing code and, of course, when reviewing a colleague’s code.

2 - How to calculate the efficiency of an algorithm with Big O

When we calculate the efficiency of a Big O algorithm, we do it by focusing on the number of steps, but in a special way.

2.1 - What does O(N) mean in big O notation?

For example, in the previous case, we said that in a linear search of an array with 200 elements, it can take up to 200 steps, and if there are 400 elements, it would take 400 steps.

This means that for the linear search algorithm, there will be as many steps as there are elements. If we convert this information into mathematics, we realize that “complexity = n”, where “n” is the number of elements.

In Big O terminology, this is expressed as "O(N)", which also means that the algorithm will have linear runtime. If you input 10 elements, it will take 10 steps, and if you input 100, it will take 100 steps.

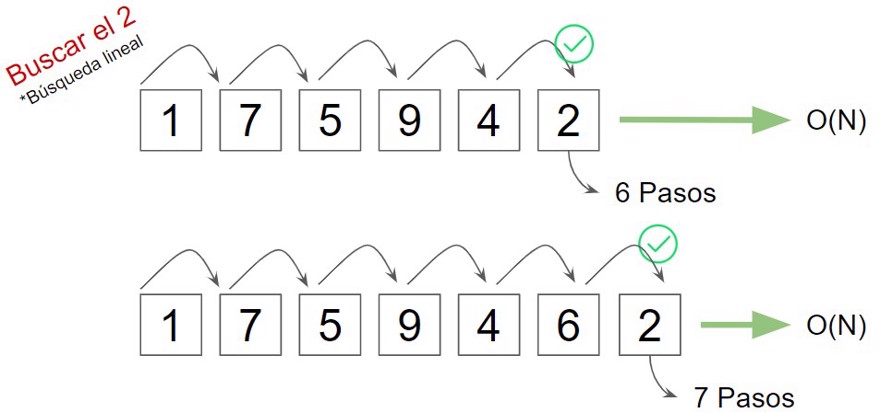
Therefore, as we see in the image, both processes are in the O(N) category, even though one has an extra step. When we define big O, we do it relative to its input data.

We can say that O(N) has a number of steps proportional to the number of input elements.

2.2 - What does O(1) mean in big O notation?

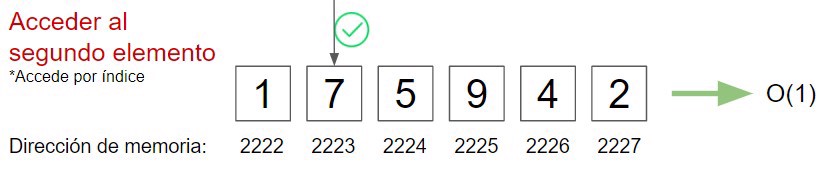
With the previous information, we can deduce that O(1) is a single step, and we see this result when we access an array by index, since an array assigns the physical memory of the computer consecutively when it is instantiated.

For example, for an array of 6 elements where its first memory address is 2222, the second will always be 2223 (2222 + 1), so by doing array[1] we only need one step to obtain the result.

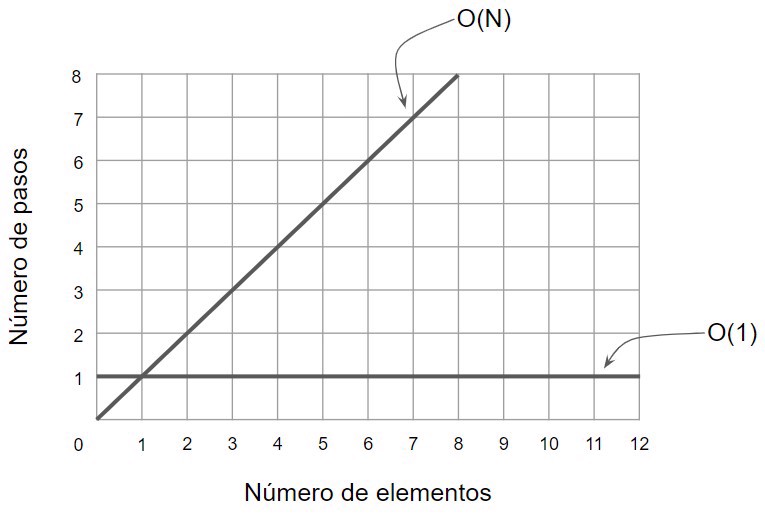
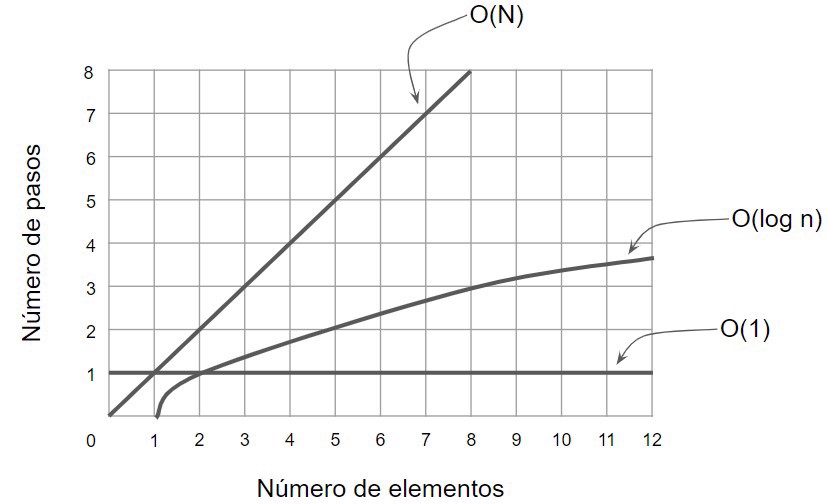
Therefore, we can compare both types of algorithms on a graph:

2.3 - What does O(log n) mean in big O notation?

We have just seen that O(1) is used when it’s a single step, and O(N) when it’s as many steps as there are input elements.

But these aren’t the only types. For example, if we have an array of sorted integers and we want to find a number, we have two options: search one by one using linear search or, alternatively, perform a binary search, where we compare the middle element to see if it’s greater or less and then repeat this process on a subgroup.

We repeat the process until we find the result.

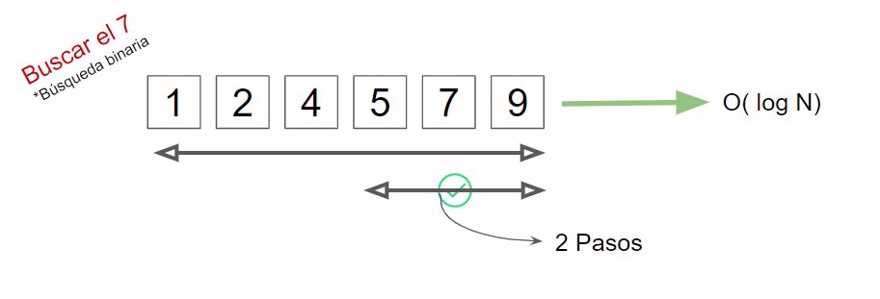
In this example, as we can see, using binary search only took two steps, while with linear search it would have taken 5.

This is because each time we halve the number of elements we need to check.

For example, a binary search with 100 elements in the worst case takes 7 steps, while a linear search would take 100.

2.3.1 - What are Logarithms?

Before continuing, just a quick note: "log" is short for logarithm.

Logarithms are the inverse of exponents. As we recall, an exponent is to "raise" a number, for example, 23 means 2*2*2 with the result 8.

So the opposite would be a logarithm, which is how many times you have to divide the number by 2 until you get 1. 8/2/2/2 = 1, which translates to log2 8 = 3.

Note: when we indicate big O notation, we omit the small 2 since it would be redundant.

2.4 - What does O(N²) mean in big O notation

When we calculate big O, it’s always according to the input parameters. So far, we’ve seen O(1) when it’s a single step, O(N) when it’s as many steps as elements, and O(log n) when we halve the number of elements at each step.

But the opposite is also possible, instead of reducing, it doubles, for example, in a bubble sort algorithm.

In the bubble sort algorithm, we compare the first element with the second, and if the first is greater, we swap them. We must do this process as many times as there are elements in the array, and we do it over the entire array.

In programming terms, it’s a for loop inside another for loop.

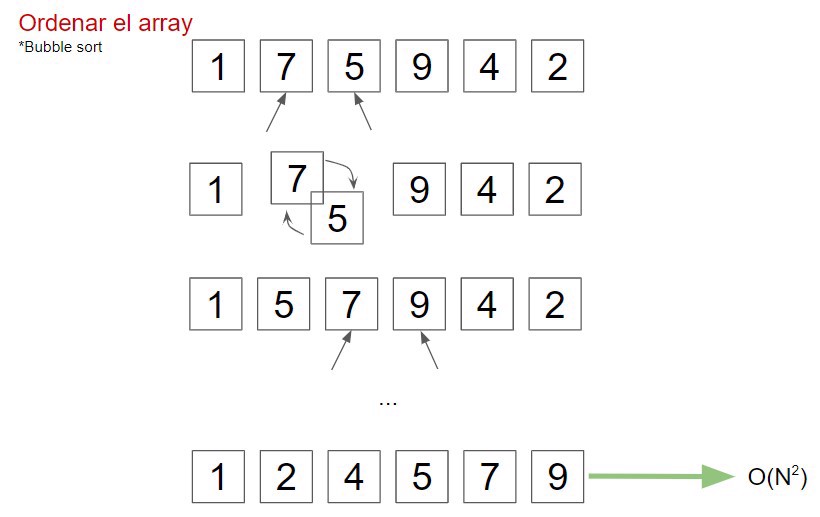
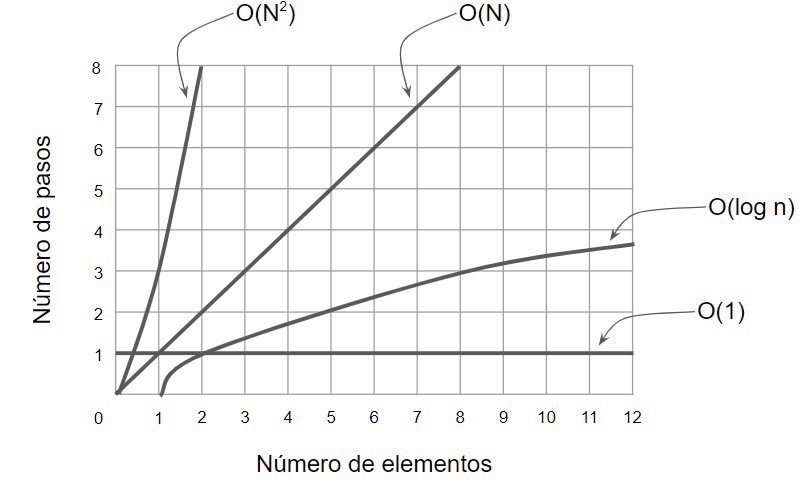
This type of algorithm is much slower than O(N) and also has a special name: quadratic algorithm.

Note: if you have 3 nested loops, it would be o(n3) as you can see, you can expand as needed. However, every exponent added makes it slower and slower. That one is called a cubic algorithm.

2.5 - Multiple data sets in big O notation

When we build algorithms, we don’t always have just one input array; very often, there can be two or even more.

We can also measure these cases. For two input arrays, it would be O(N*M); however, on a graph, we don't really know how to draw it. It simply falls somewhere between O(N) and O(N2) knowing that if both arrays have the same size, it would be O(N2).

The same would apply if we had 3 arrays; it would fall somewhere between O(N) and O(N^3) on the chart.

3 - Subgroups within the same type of algorithm

Choosing the big O notation is important, as it groups different algorithms. But that's not the end: take into account not every algorithm in the same category has to be exactly the same.

I previously mentioned in the case of logarithms that they’re really log₂ but that we remove the 2.

Well, the same thing happens when we have an algorithm that takes half of n; we could write it as O(N/2), or one that takes twice as long O(2N). In both we remove the two (or whatever the number is) for simplicity, which causes both algorithms to fall under the same group O(N).

This can be seen more clearly with two algorithms: "selectionSort" and "insertionSort"

The first is a O(N2) algorithm, but in reality it is O(N2/2):

public static int[] SelectionSort(int[] array)
{
    for (int i = 0; i < array.Length - 1; i++)
    {
        int lowestNumberIndex = i;
        for (int j = i + 1; j < array.Length; j++)
        {
            if (array[j] < array[lowestNumberIndex])
            {
                lowestNumberIndex = j;
            }
        }
        if (lowestNumberIndex != i)
        {
            int temporal = array[i];
            array[i] = array[lowestNumberIndex];
            array[lowestNumberIndex] = temporal;
        }
    }
    return array;
}

While the second is also a O(N2) algorithm, but actually is O(N2 +N).

public static int[] InsertionSort(int[] array)
{
    for (int i = 1; i < array.Length; i++)
    {
        int valueToCompare = array[i];
        for (int k = i-1; k >= 0; k--)
        {
            if (array[k] > valueToCompare)
            {
                array[k+1] = array[k];
            }
            else
            {
                break;
            }
            array[k] = valueToCompare;
        }
    }
    return array;
}

This characteristic means we can very quickly identify what type of algorithm we are looking at, but if there is more than one option in the same category, we should spend time looking closely at exactly how the algorithm works inside.

3.1 - How to identify Big O in code

To determine the main group or category an algorithm falls into, we should look at two important aspects.

1 - The number of input elements

This helps us identify if it’s O(n), o(n*m), etc.

2 - The number of loops that refer to the input element

To place it in a category, we do not take into account the arithmetic operations it contains, only the loops that refer to the input element.

For example, if you have a loop that prints “hello” 10 times for each input element, we must not consider it for big O notation, since it is a static element that never changes.

Conclusion

• In this post, we’ve seen what big O notation is as well as some of its different types.
• We’ve seen how to identify big O notation in code.
• Personally, I would say that while in day-to-day work it’s not as important, in job interviews it certainly is.
• Of course, in some cases where we need highly optimized code to handle large loads, understanding big O notation will help us better understand code flow and, consequently, the time or load it will support.